Omitted-variable bias
In statistics, omitted-variable bias (OVB) occurs when a model is created which incorrectly leaves out one or more important causal factors. The 'bias' is created when the model compensates for the missing factor by over- or under-estimating one of the other factors.
More specifically, OVB is the bias that appears in the estimates of parameters in a regression analysis, when the assumed specification is incorrect, in that it omits an independent variable (possibly non-delineated) that should be in the model.
Omitted-variable bias in linear regression
Two conditions must hold true for omitted-variable bias to exist in linear regression:
- the omitted variable must be a determinant of the dependent variable (i.e., its true regression coefficient is not zero); and
- the omitted variable must be correlated with one or more of the included independent variables.
As an example, consider a linear model of the form
where
- xi is a 1 × p row vector, and is part of the observed data;
- β is a p × 1 column vector of unobservable parameters to be estimated;
- zi is a scalar and is part of the observed data;
- δ is a scalar and is an unobservable parameter to be estimated;
- the error terms ui are unobservable random variables having expected value 0 (conditionally on xi and zi);
- the dependent variables yi are part of the observed data.
We let
and
Then through the usual least squares calculation, the estimated parameter vector 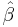 based only on the observed x-values but omitting the observed z values, is given by:
based only on the observed x-values but omitting the observed z values, is given by:
(where the "prime" notation means the transpose of a matrix).
Substituting for Y based on the assumed linear model,
On taking expectations, the contribution of the final term is zero; this follows from the assumption that U has zero expectation. On simplifying the remaining terms:
The second term above is the omitted-variable bias in this case. Note that the bias is equal to the weighted portion of zi which is "explained" by xi.
Effects on Ordinary Least Square
Gauss–Markov theorem states that regression models which fulfill the classical linear regression model assumptions provide the best, linear and unbiased estimators. With respect to ordinary least squares, the relevant assumption of the classical linear regression model is that the error term is uncorrelated with the regressors.
The presence of omitted variable bias violates this particular assumption. The violation causes OLS estimator to be biased and inconsistent. The direction of the biased depends on the estimators as well as the covariance between the regressors and the omitted variables. Given a positive estimator, a positive covariance will lead OLS estimator to overestimate the true value of an estimator. This effect can be seen by taking the expectation of the parameter, as shown in the previous section.
References
- Greene, WH (1993). Econometric Analysis, 2nd ed.. Macmillan. pp. 245–246.
- Barreto and Howland (2005). Introductory Econometrics: Using Monte Carlo Simulation with Microsoft Excel. Cambridge University Press. http://www3.wabash.edu/econometrics/EconometricsBook/chap18.htm.
|
|||||||||||
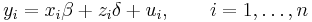
![X = \left[ \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right] \in \mathbb{R}^{n\times p},](/2012-wikipedia_en_all_nopic_01_2012/I/6a852b783d056c37d9d82a99a74a598a.png)
![Y = \left[ \begin{array}{c} y_1 \\ \vdots \\ y_n \end{array} \right],\quad Z = \left[ \begin{array}{c} z_1 \\ \vdots \\ z_n \end{array} \right],\quad U = \left[ \begin{array}{c} u_1 \\ \vdots \\ u_n \end{array} \right] \in \mathbb{R}^{n\times 1}.](/2012-wikipedia_en_all_nopic_01_2012/I/728711b2ec4afef6fb7988583dd5c3e2.png)
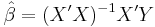
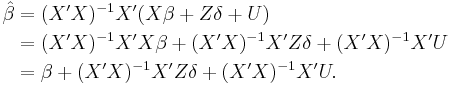
![\begin{align}
E[ \hat{\beta} | X ] & = \beta %2B (X'X)^{-1}X'Z\delta \\
& = \beta %2B \text{bias}.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/ba8ffe4a20aa7d1f8fc96f7000f7c810.png)